Здавалось би, що може бути дивніше за комплексні числа? – гіперкомплексні числа.
Ця штука була винайдена в 1843 році Гамільтоном як основний метод розвʼязку завдань про числа Гамільтона.
Вся ця складна магія описується дуже простою формулою:
i² = j² = k² = ijk = -1
Цей вираз варто поділити на 3 частини перед тим, як почнемо його розбирати:
i² = j² = k²ijk-1
Як воно працює? Давайте розберемось
Частина 1 та 3
Як і в комплексних числах, гіперкомплексні числа мають такі ж властивості, за вийнятком, що їх три, а не одне.
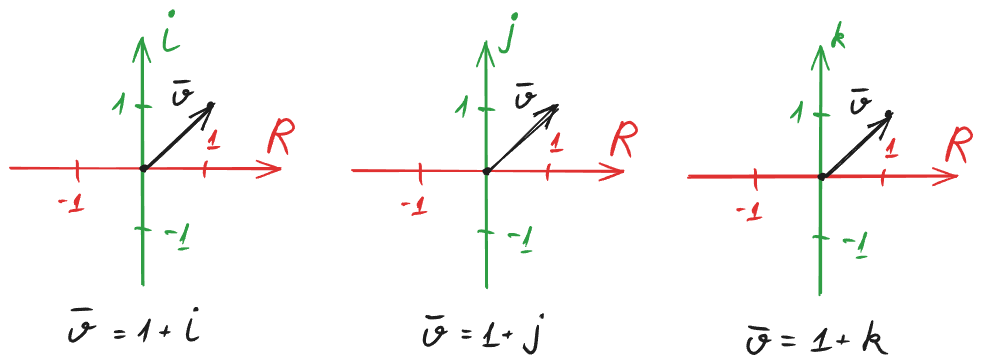
Такий підхід показує нам розміщення вектора в двовимірному просторі. В ньому використовуються осі дійсних та уявних чисел.
При цьому варто памʼятати, що
i² = j² = k²
Алеi != j != k
Гамільтон викинув вісь дійсних чисел та обʼєднав три уявні осі в три площини для візуалізації тривимірного простору.
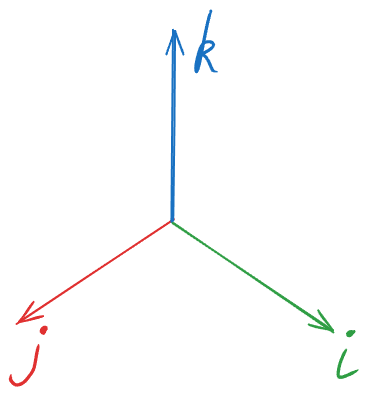
Знаючи властивості комплексних чисел, виникає запитання, а як ми можемо здійснити обертання в просторі, якщо у нас, наприклад, i² = -1 але осі з дійсними числами на площинах нема? До цього повернемось трохи пізніше. Зараз розглянемо нові властивості, що у нас зʼявились із таким підходом:
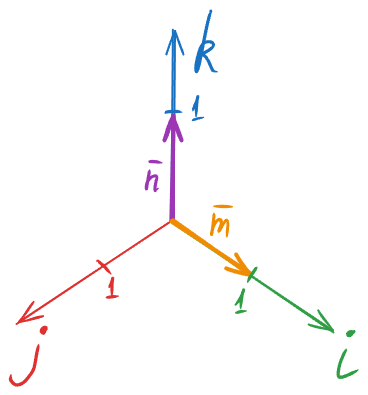
Уявімо, що на осі i та k ми розмістили вектори: m та n, і в кожного з них довжина 1.
Давайте відобразимо координати наших векторів:
n = 1km = 1i
І тепер давайте спробуємо здійснити операцію множення над цими векторами:
n * m = ?
Як думаєте, яким буде результат операції?
На даному етапі пропоную зупинитись та запропоновувати собі в голові хоча б одне рішення, а потім продовжити прочитання статті.
Давайте, здійснимо невелике повернення в часі до звичайної векторної алгебри.
Добуток двох векторів (векторний добуток, не скалярний!) у тривимірному просторі завжди даватиме в результаті третій вектор, перпендикулярний до попередніх двох:
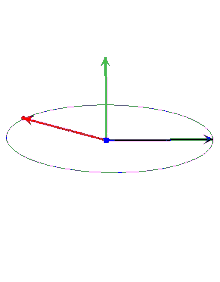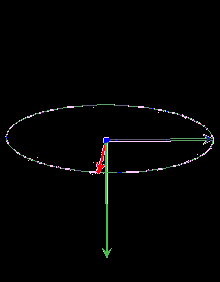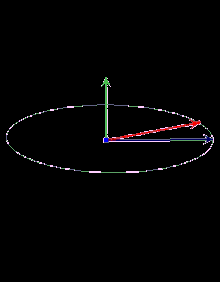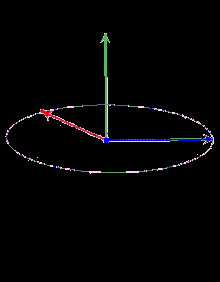
І саме кут між векторами, що множаться, впливає на довжину і напрямок вектора, що є результатом даної операції.
Аналогічно і в гіперкомплексних числах: якщо ми здійснюємо операцію множення двох векторів, що знаходяться в гіперкомплексній площині, то в результаті отримаємо третій вектор, перпендикулярний до попередніх двох:
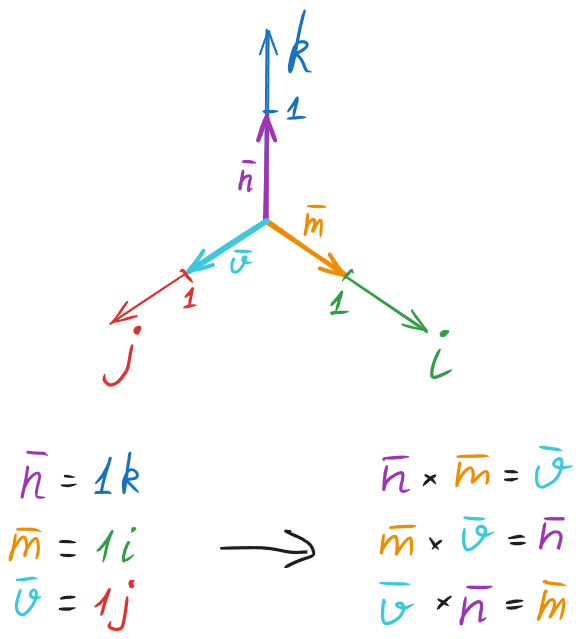
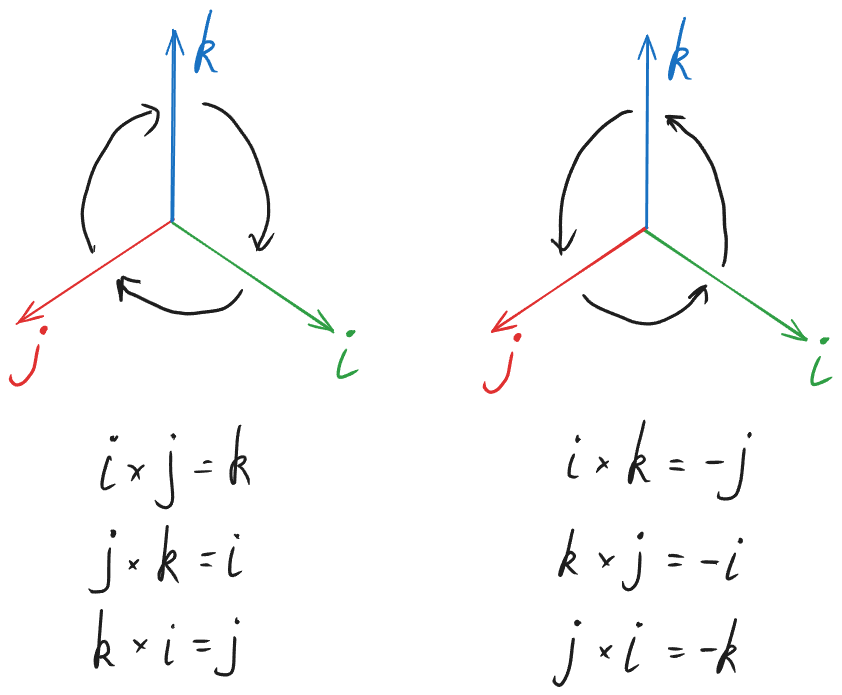
З цього можемо вивести просту залежність:i * j = kj * k = ik * i = j
Сподіваюсь, із цим питань не виникає? Якщо так – раджу перечитувати текст вище до того моменту, поки не зрозумієте суть цих операцій.
Якщо все зрозуміло, рухаємось далі.
Дуже важливим нюансом у всій цій математиці є те, що ці операції множення не є комутативними.
Некомутативні операції, це коли:
m * n != n * m
Або
m×n=−(n×m)
Простішими словами кажучи, якщо ми поміняємо множник і множене місцями, то результат буде відрізнятись. Результат буде з протилежним знаком.
Для нас це означає, що
m * n = v, а n * m = -v
На гіперкомплексній площині це виглядатиме наступним чином:
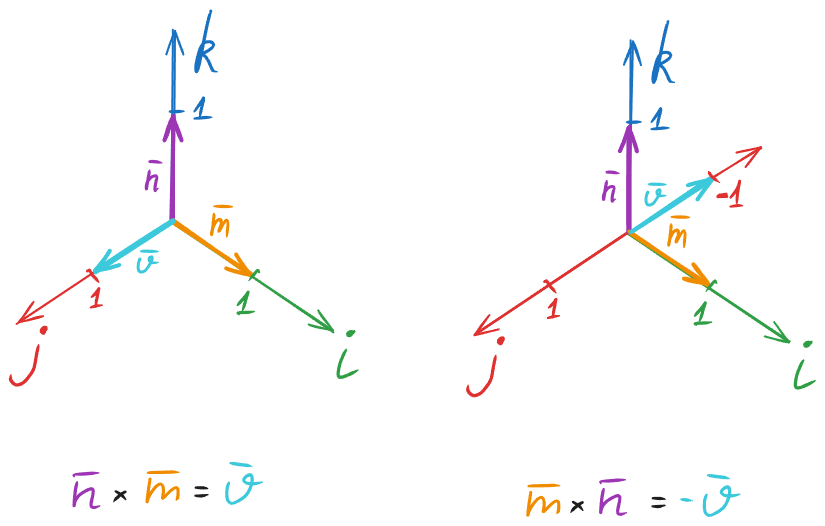
З цього можна зробити висновок:
Частина 2
Як ось це: i² = j² = k² може бути рівне цьому: ijk і є рівним -1?
Давайте розглянемо саме вираз ijk. Ми вже знаємо, що i * j = k. Отже це можна записати як i * j * k = k * k = k² = -1.
Сподіваюсь, це пояснення було цілком доступним.
Якщо ви, як і я в свій час, задаєтесь питанням, а чому воно працює саме так, і ваш внутрішній чомучка закидує питанням “звідки це все взялось?”, раджу на даному етапі сприймати все як аксіому. Цей підхід Гамільтоном був вибраний не спроста.
Ви ще можете запитати, “а чим це відрізняється від звичайної векторної алгебри? – логіка роботи така ж”. Для чого на вже існуючу систему натягувати нові букви, придумувати їм дивні правила виконання, а потім сказати, що це вже описано в іншому розділі математики і воно працює так же?
Ви праві і не зовсім водночас. В такому підході до розрахунку орієнтації у нас є ще четвертий стан, про який ми згадували раніше. А що буде, якщо i² = j² = k² = -1? Як це відобразити на цих площинах?
Відповідь вас може вразити: ніяк.
Гіперкомплексна площина – це чотиривимірна площина, яку неможливо зобразити на тривимірному просторі повноцінно. Уявити теж неможливо:(
Множина дійсних чисел не може бути представлена на малюнках вище.
Найкраще наблизитись до розуміння можна через кватерніони.
Але це вже зовсім інша історія:
[[8 Частина 1. Зміна підходу до розрахунку орієнтації в просторі]]