Урок
Комплексні числа. Чи бачили ви коли-небудь вираз
i² = -1?
Людині, яка не бачить практичного застосування цієї математичної концепції, дуже важко осягнути й зрозуміти, як вона працює і навіщо потрібна.
Комплексні числа вперше застосували для розв’язування кубічних рівнянь у XVI столітті.
Проте формалізація та приведення цього розділу математики до сучасного вигляду тривали кілька століть.
На початку XIX століття математики вперше зобразили комплексні числа на декартовій площині. Це відкрило простий спосіб обертання об’єктів у просторі, що докорінно змінило людське уявлення про світ.
“ЯК КОМПЛЕКСНІ ЧИСЛА ОБЕРТАЮТЬ ОБ’ЄКТИ В ПРОСТОРІ? НУ ПОЯСНІТЬ ХТО НЕБУДЬ”
Саме така думка виникає при вивченні даної теми.
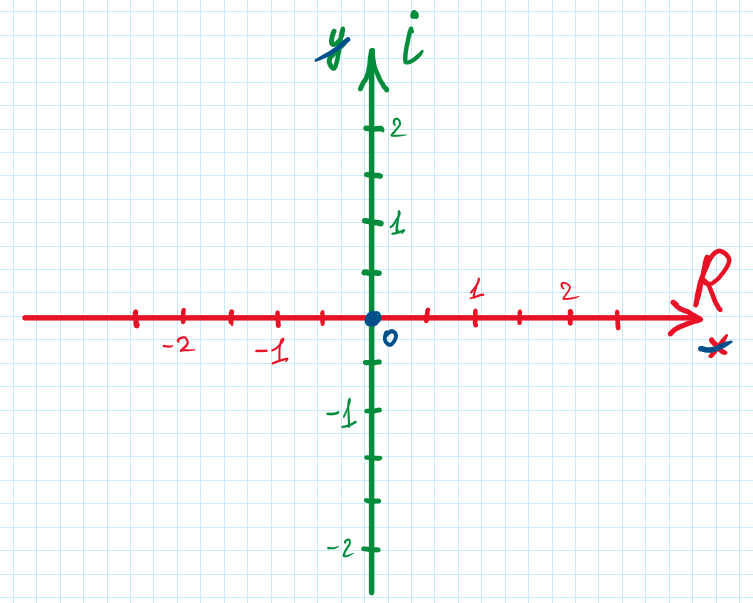
Декартова площина на яку наносять комплексні вирази – це комплексна площина (X та Y закреслені, бо вони більше не потрібні).
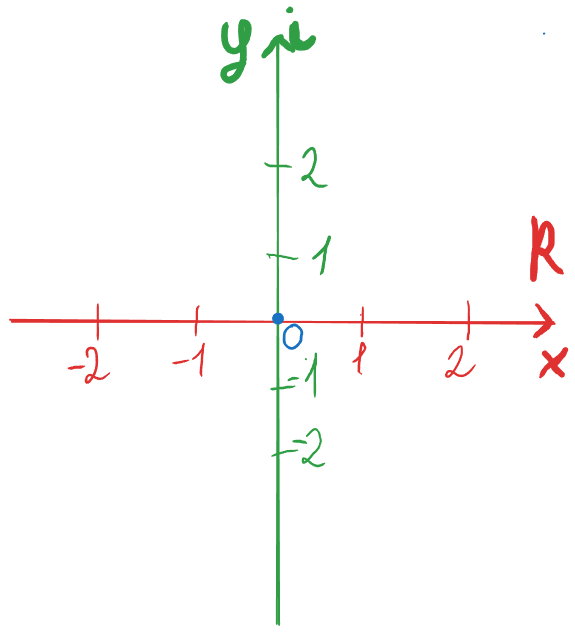
R – дійсні числа (звичні для нас числа)
i – комплексні числа (…-2i, -1i, 0, 1i, 2i, 3i…)
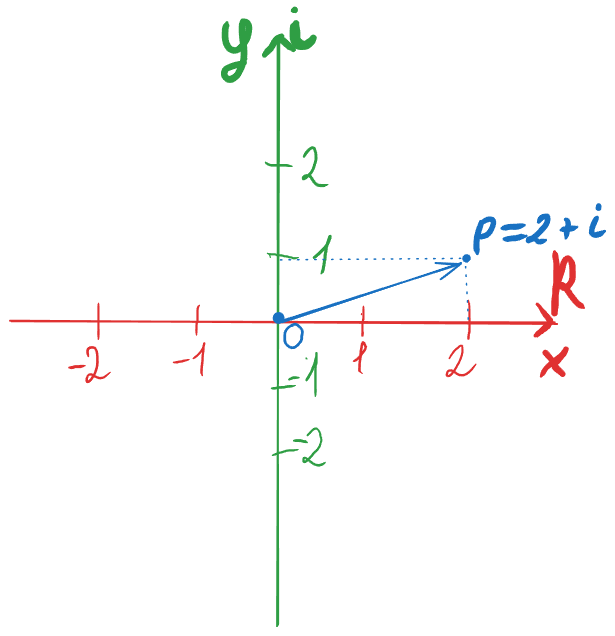
Тепер давайте спробуємо нанести щось на дану площину. Нехай це буде точка p
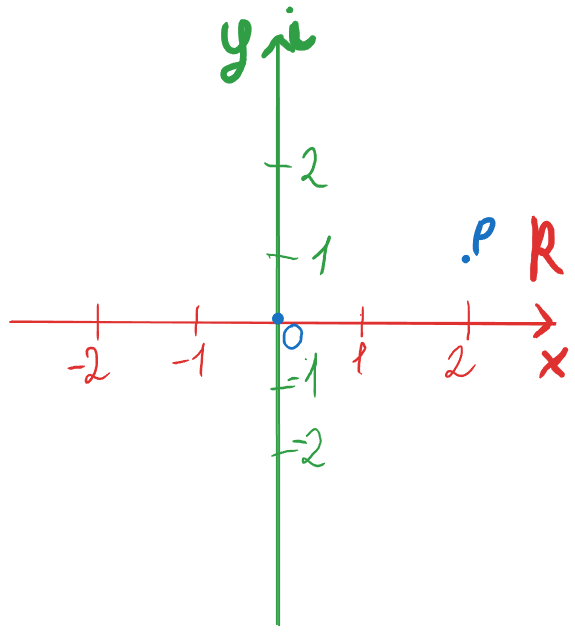
Ми бачимо розміщення цієї точки, але давайте спробуємо записати точні координати.
Для цього проведемо штриховані лінії до двох осей:
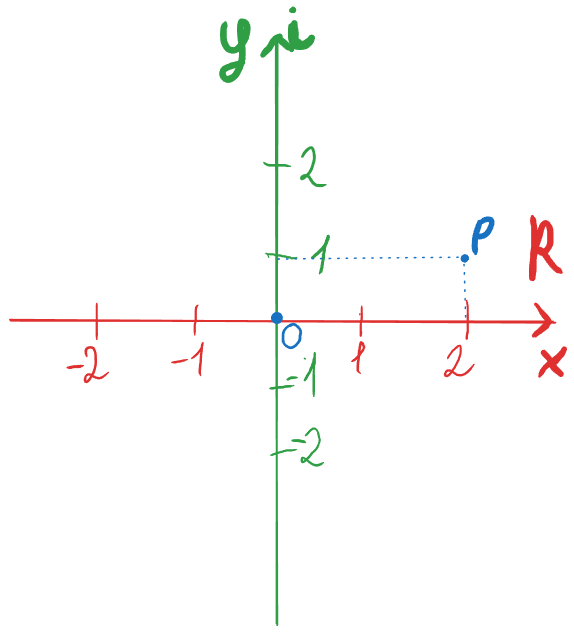
Як бачимо, на осі дійсних чисел у нас додатнє число 2. На осі уявних чисел у нас додатнє число 1i (1 можемо не вказувати). Отже можемо записати координати точки як:
p = 2 + i
Уявимо, що точка p – не одинока точка в просторі, а це кінець вектора (спрощуємо собі життя на майбутнє для кращого розуміння кутів, на які відбувається обертання).
Отже, математика – наш торт, i – наша вишенька.
Що буде, якщо ми домножимо координати, що описують точку p на ще одне число i?
Давайте спробуємо розв’язати:
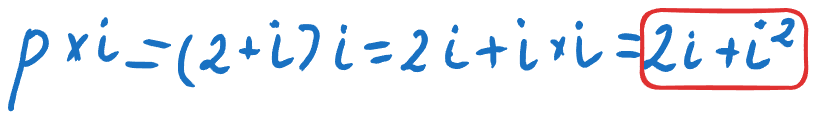
І що це ми бачимо? i² ? Давайте повернемось на початок і згадаємо вираз *i² = -1
Що робимо? Звісно міняємо i² на `-1
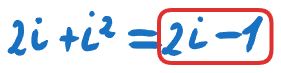
Нанесемо точку на графік? А давайте. І назвемо її q
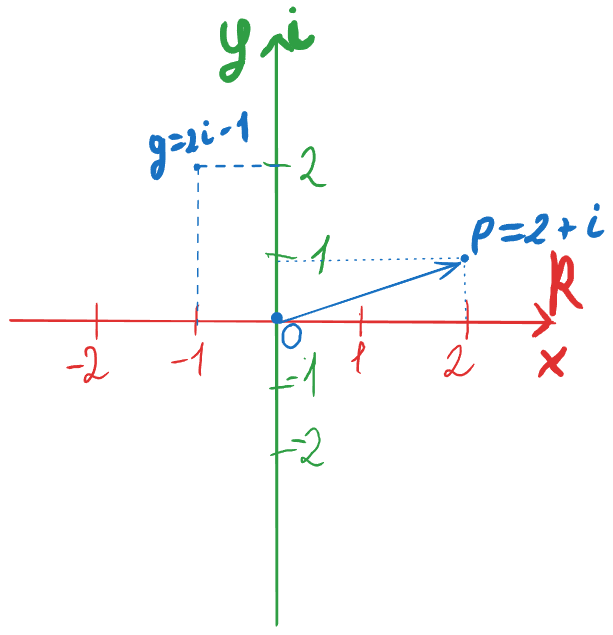
Здогадуєтесь вже? Давайте проведемо вектор до точки q
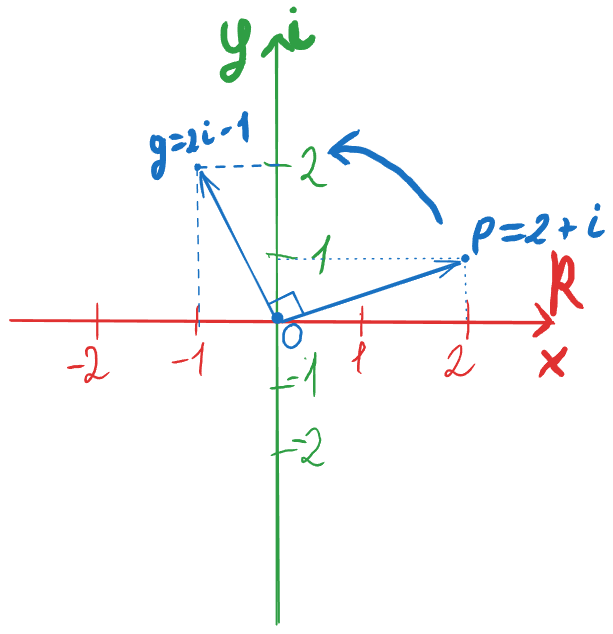
І що ми бачимо? Наш вектор, кінцева точка якого p, змінив свій напрямок на 90° проти годинникової стрілки і зупинився в точці q