std::learn

2.2 Система керування. Основа орієнтації в просторі.

—

від

Коржак Богдан
у

План уроку

  • Основи орієнтації в просторі. Кути Ейлера
  • Використання кутової швидкості для розрахунку орієнтації в просторі

Матеріали

  • ESP32 – 10 шт
  • IMU MPU6050 – 10 шт
  • Провідники 4-х кольорів, 26AWG, по 10 м.
  • Паяльники
  • Припій. Флюс/каніфоль

Результат уроку

Результатом даного уроку має бути:

ESP32 із MPU6050, що вимірюють прискорення та кутову швидкість, і розраховують орієнтацію в просторі методом інтегрування Ейлера.

Урок

Основи орієнтації в просторі. Кути Ейлера

Орієнтація об’єкта в просторі – це його положення відносно глобальної системи координат.
Нижче на зображенні представлено дві системи координат: глобальну (XY) та локальну (xy). Локальна система координат (ЛСК) прив’язана до об’єкта (Nokia 3310:D), що знаходить в Глобальній системі координат (ГСК).

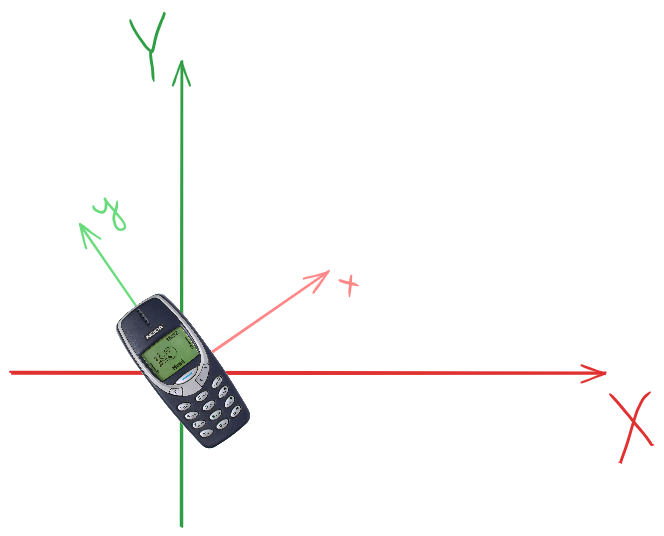
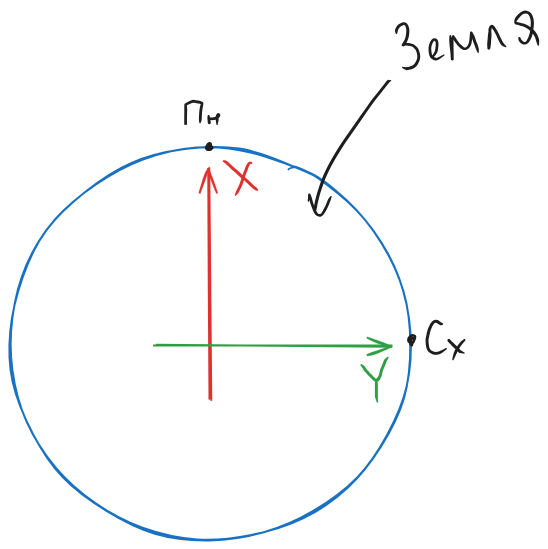
Глобальною системою координат може виступати наша планета, осі якої будуть розміщені відповідно сторонам світу, при цьому прошу звернути увагу, що вісь X завжди направлена на Північ, а Y – Схід.

Кути Ейлера (названі на честь швейцарського математика Леонарда Ейлера) – це спосіб описати орієнтацію об’єкта в тривимірному просторі за допомогою трьох кутів:

  1. Крен, або roll, позначається грецькою літерою φ
  2. Тангаж, або pitch, позначається грецькою літерою θ
  3. Рискання, або yaw, позначається грецькою літерою ψ

Як це працює?

  1. Крен (φ): Обертання навколо поздовжньої осі (X).
  2. Тангаж (θ): Обертання навколо поперечної осі (Y).
  3. Рискання (ψ): Обертання навколо вертикальної осі (Z).

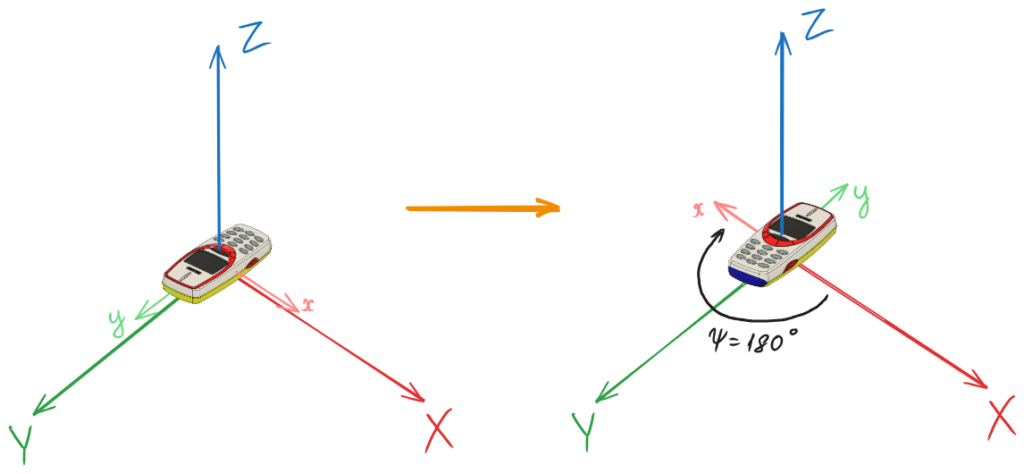
На зображенні вище представлено обертання об’єкта навколо осі Z (по рисканню) на 180°

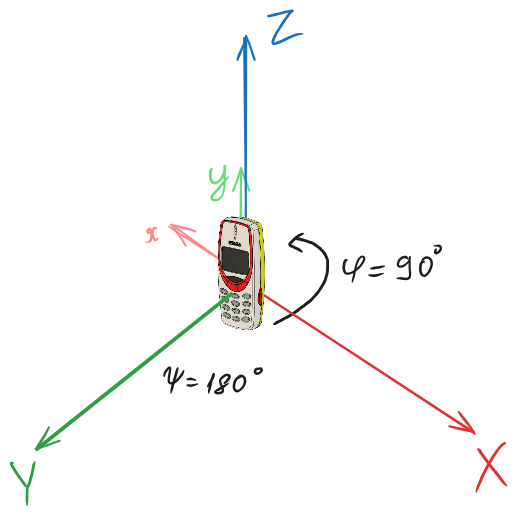
Так само можна обертати об’єкт і по інших осях, наприклад Х, зберігаючи попередні обертання:

Де застосовується?

Кути Ейлера широко використовуються в:

  • Авіації та космонавтиці
  • Робототехніці
  • Комп’ютерній графіці та анімації
  • Навігаційних системах

Наприклад, в авіації:

  • Крен – нахил літака вліво або вправо
  • Тангаж – підйом або опускання носа літака
  • Рискання – поворот літака вліво або вправо

Для кращого розуміння логіки обертання об’єкта в просторі було створено програму RotationVisualiser, що дозволяє візуалізувати в реальному часі зміну орієнтації об’єкта в просторі:

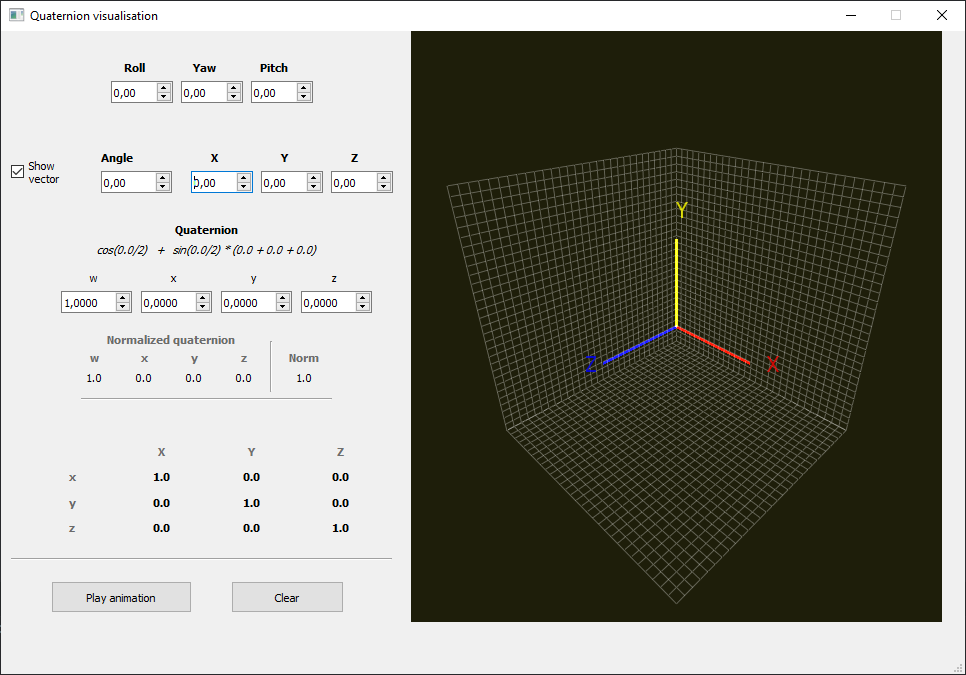
Змінюючи наступні параметри ми зможемо змінювати орієнтацію об’єкта:

Наприклад, зміна орієнтації по Рисканню на 45° провертає тригранник навколо осі Y на визначений кут:

Використання кутової швидкості для розрахунку орієнтації в просторі

Коли автомобіль рухається з точки А в точку Б, на його спідометрі можна побачити виміряну швидкість. Ця швидкість є лінійною (грубо кажучи, можна вважати, що авто рухається вздовж лінії), і вимірюється в км/год, або за системою СІ – м/сек

Але крім лінійної швидкості фізики виділяють ще кутову швидкість.
Коли ми крутимо спінер, навколо однієї його осі виникає кутова швидкість, з якою вся конструкція обертається по-колу.

Кутова швидкість – це величина, яка описує, як швидко об’єкт обертається навколо певної осі. Якщо ви вже розумієте орієнтацію в просторі, то можна уявити кутову швидкість як швидкість зміни цієї орієнтації з часом.

Ключові аспекти кутової швидкості:

  1. Вимірювання: Кутова швидкість зазвичай вимірюється в радіанах за секунду (рад/с) або градусах за секунду (°/с).
  2. Напрямок: Кутова швидкість є векторною величиною. Її напрямок відповідає осі обертання згідно з правилом правої руки.
  3. Приклади:
    • Секундна стрілка годинника має кутову швидкість 6°/с або π/30 рад/с.
    • Земля обертається навколо своєї осі з кутовою швидкістю приблизно 7.27 * 10^-5 рад/с.

Як використовувати кутову швидкість?

Для початку, пригадаймо зв’язок між лінійною швидкістю та пройденою відстанню:

  1. Для лінійного руху:

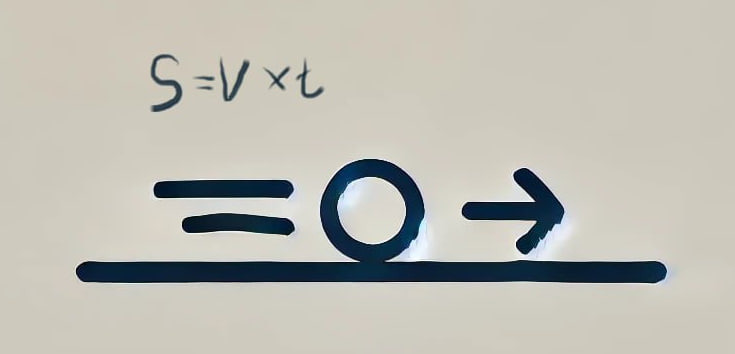
    • Відстань = Швидкість * Час
    • s = v * t

  2. Для обертального руху аналогічно:

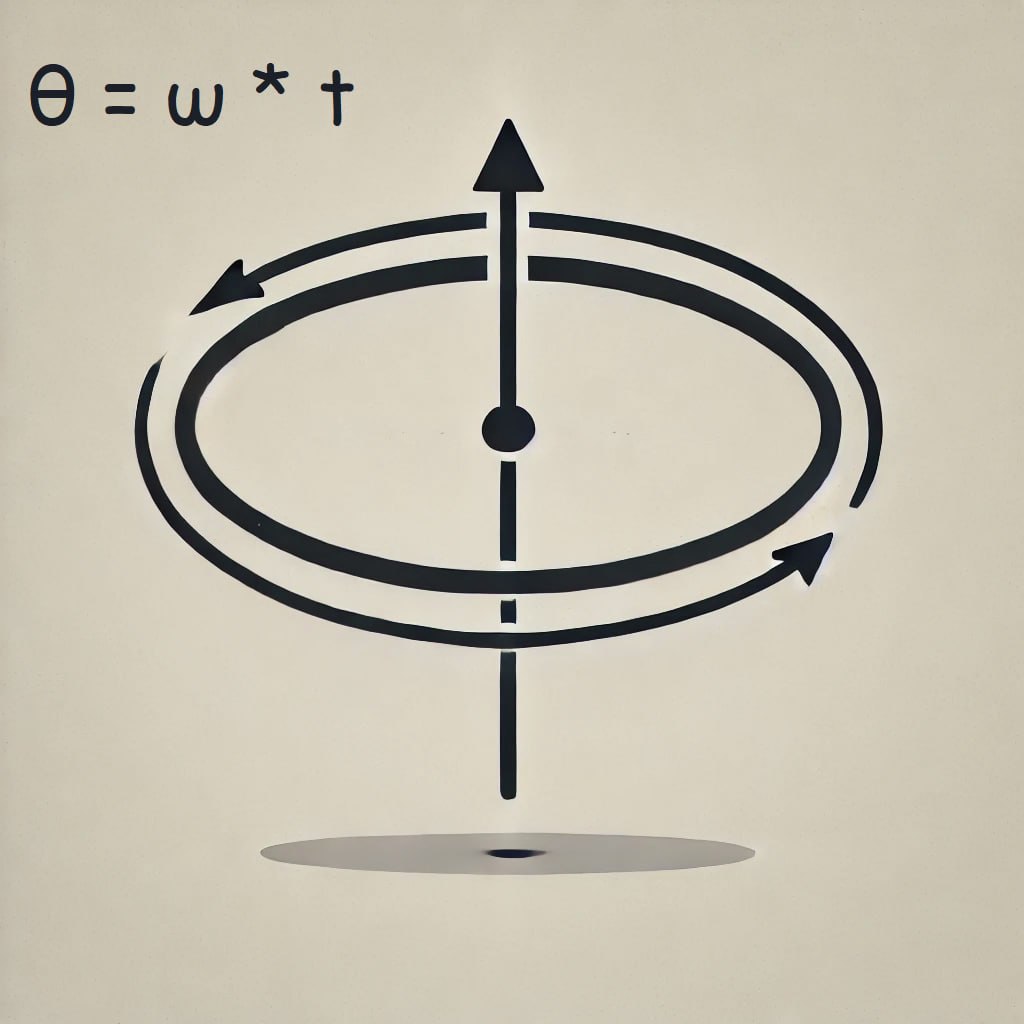
    • Кут = Кутова швидкість * Час
    • θ = ω * t

де θ (тета) – кут у радіанах, ω (омега) – кутова швидкість у радіанах за секунду, t – час у секундах.

Щоб краще зрозуміти це, розглянемо паралелі:

  1. Лінійна швидкість (v) вимірює, як швидко об’єкт проходить відстань. Кутова швидкість (ω) вимірює, як швидко об’єкт проходить кут.
  2. Лінійна швидкість вимірюється в метрах за секунду (м/с). Кутова швидкість вимірюється в радіанах за секунду (рад/с).
  3. Пройдена відстань (s) вимірюється в метрах (м). Пройдений кут (θ) вимірюється в радіанах (рад).

Даний спосіб розрахунку кута із кутової швидкості називається інтегруванням Ейлера

Додаткове ПЗ

RotationVisualiser

Додаткові посилання

Гіроскопічний ефект

Відеоуроки та записи уроку

Урок 1- Гіроскоп та акселерометр